Introduction
Nearly all stellar evolutionary calculations are calibrated with respect to a standard solar model. The standard solar model is derived from the conservation laws and energy transport equations of physics, applied to a spherically symmetric gas (plasma) sphere, constrained by the luminosity, radius, age and composition of the Sun. The standard solar model is used as a test case for the stellar evolution calculation because the luminosity, radius, age and composition of the Sun are well determined. In fact, the only way to determine the two free parameters of the stellar evolution calculation, viz. the helium abundance and the mixing length parameter, is to adjust the standard solar model to "fit" the observed Sun.
To obtain the standard solar model, a one solar mass, zero age stellar model (a model with a homogeneous distribution of chemical elements which is just beginning to derive most of its luminosity from nuclear reactions) is evolved to the age of the Sun. The structural changes in the Sun, as it evolves, are caused by the nuclear reactions occurring in the central regions of the Sun. The transmutation of four hydrogen atoms into one helium reduces the number density of particles in the central regions which decreases the pressure. The pressure decrease does not actually occur because the surrounding layers respond to the force imbalance by contracting in towards the center. Half of the gravitational energy released from the contraction goes to raising the temperature of the central regions (the other half, according to the Virial Theorem, is radiated away). The increased temperature, by the ideal gas law, increases the pressure of this region and restores the balance between the pressure and gravitational forces. The increased mean molecular weight increases the luminosity of the star, and the rate of nuclear reactions. Also, while the central layers contract, the outer regions expand, in a sense, compensating for the steepening temperature gradients in the central regions (in fact, the temperature gradients are simply adjusting themselves to maintain energy flow to the surface). Therefore, as the Sun evolves from the zero age both its luminosity and radius increase.
The definition of the standard model depends critically on fitting the model to some of the Sun's observable characteristics. The one solar mass model must have the observed radius and luminosity of the Sun at the Sun's inferred age. In addition, the model's surface composition of hydrogen to heavy elements ratio must match the observed solar abundances. Even though both the Sun's neutrino flux and the p-mode oscillation spectrum have been measured, they are not normally used to constrain the definition of the standard solar model. In fact, as is well known, the standard solar model produces significantly more neutrinos than are observed by the Davis experiment (1978). Also, the p-mode frequencies of the standard solar model do not precisely match (the error is of the order of ±0.1%) the observed frequencies.
The standard solar model serves two purposes: (1) it provides estimates for the helium abundance and mixing length parameter in the Sun by forcing the solar model to have the correct luminosity and radius at the Sun's age, and (2) it provides a laboratory to test new physics and compare "improved" solar models which have additional physics, such as rotation, magnetic fields, and diffusion or ad-hoc improvements, such as turbulent diffusion, overshooting, and metal rich cores. The former role comes about from the fact that neither the helium abundance nor the mixing length parameter can be precisely determined from observation or laboratory experiment. As a consequence, many stellar evolutionary calculations of Pop. I stars assume a solar mixing length parameter and a solar helium abundance.
Basic Physics
The most firmly grounded laws used in modeling the evolution of the Sun from zero age to its current age are the conservation laws of physics, viz. the conservation of mass, momentum, and energy. These three laws along with the energy transport equation and the equations describing the nuclear reaction network constitute the complete set of equations which describe the evolution of a star. They are discussed at length in all books on stellar structure and evolution. Some classic books on the theory of stellar structure and evolution, in addition to the landmark books by Eddington (1926) and Chandrasekhar (1939), are Schwarzschild's Structure and Evolution of the Stars (1965), Clayton's Principles of Stellar Evolution and Nucleosynthesis, (1968), and Cox and Giuli's Principles of Stellar Structure (1968). Most modern textbooks base their stellar theory chapters on these original volumes (unfortunately, the newer texts all too often introduce errors).
In the standard solar model the physics is simplified by assuming that the Sun is spherically symmetric. The symmetry breaking physics of magnetic fields and rotation are neglected because they increase the complexity of the problem enormously and are generally not believed to affect the structure and evolution of the model by very much. We note that the energy arguments used to prove the unimportance of magnetic fields and rotation are based on the surface values of these quantities. It is possible that magnetic fields and rotation in the interior are orders of magnitude stronger.
The amount of mass converted into energy over the entire life time of the star is less than 0.007 the total mass of the nuclear burning regions of the star and thus can be ignored. Also, in current standard solar models, mass loss from winds is usually not included, again, because the loss is considered negligible (1.0E-14 Msun/year Cassinelli and MacGregor, 1986) when compared to the total mass. The total mass and the mass in any given layer is, therefore, assumed to be constant during the evolution of the Sun. Substantial mass loss, of the order of several tenths of a solar mass, occurs much later in the life of the solar-type star.
The dynamical time scale of the Sun is approximately one hour, hence, during the Sun's 4.5 Gyr lifetime it has had more than enough time to establish hydrostatic equilibrium. For any volume element within the Sun the weight of the element is assumed to be exactly balanced by the sum of all pressure forces acting on the element. The total pressure includes both the gas pressure and the radiation pressure. In the Sun, the radiation pressure at the center accounts for only 0.05% of the total pressure.
The energy balance of any shell in the Sun is obtained by equating the sum of the energy entering the bottom of the shell and the energy produced by nuclear reactions within the shell to the sum of the energy lost through the top of the shell plus the work energy done by the shell on its surroundings. This balance is represented mathematically by:
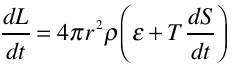
where L is the total luminosity (energy per unit time per unit area) passing outwards through the shell at radius r, epsilon is the nuclear energy generation rate per unit mass, and S is the entropy per unit mass. The T dS/dt term ("entropy term") is the sole term in the basic stellar evolution equations that includes time explicitly. It describes the internal energy gains and losses associated with the structural changes that occur as the star evolves. The structural changes, as mentioned earlier, are due to the continually occurring nuclear processes. If the entropy term were dropped then the equations would describe a static non-evolving model.
Energy Transport
Three forms of energy transport are modeled in stellar evolutionary calculations: convection, conduction, and radiation. Only convective and radiative transport are important in the Sun. It is the efficiency of the energy transport (determined by the opacity and temperature gradients in the star) which determines the overall luminosity of the star.
The relation between the temperature gradient and the power flux of photons is described by the radiative transport equation. Even though energy is clearly flowing out of the Sun the temperature gradients required to account for the Sun's luminosity are shallow enough that locally the Sun's interior can be considered to be in thermodynamic equilibrium. This permits the equations describing the radiative transport of energy to be linearized. In the Sun, this linearization is accurate to one part in 1.0E10, i.e. the neglected second order terms are 1.0E10 times smaller than the linear terms! The opacity, a function of temperature, density, and composition, is probably the least accurately determined term in the equations of stellar evolution, having an error of up to ±20%.
When the temperature gradient required to transport all the energy by radiation exceeds the adiabatic temperature gradient, the layer is unstable to convection and the material physically transports the energy outwards. Because convection is very efficient at transporting energy, the temperature gradient in the convective region needs to be only slightly superadiabatic in order for convection to carry nearly all the energy. This is not true near the surface where the density is low enough that radiative transport must be taken into account. The real temperature gradients in this thin outer layer are significantly steeper than the adiabatic temperature gradient. Except for this outer most layer, the temperature gradient in a convective region is taken to be the adiabatic temperature gradient. In the outer convection zone the process is modeled by the mixing length theory.
Analogous to Prandtl's (1952) fluid dynamical picture, the mixing length can be defined as the length traveled by a convective element before it loses its identity. In the stellar context, where there are steep pressure gradients in the convection zone, it is convenient to define a mixing length parameter alpha, which is the ratio of the mixing length to the local pressure scale height (Böhm-Vitense 1958). The original Prandtl meaning has been partially lost in stellar evolutionary calculations where alpha is used to control the radius of the model, therefore, it effectively characterizes the efficiency of energy transport by controlling the steepness of the temperature gradient in the very outer superadiabatic layer of the Sun. This gradient is adjusted, via alpha, until the radius of the model matches the observed radius of the Sun. The temperature gradient throughout the entire convective envelope is, therefore, characterized by one number. And because the flow of energy through this layer is controlled by the temperature gradient, ultimately it is the mixing length parameter which controls this flow. As a consequence, the actual temperature stratification in the convective envelope of the Sun may be different (in fact, helioseismology has proven that it is different), especially in the very outer superadiabatic region, from that predicted by the standard solar model using the mixing length theory.
The Equation of State.
The four equations in five variables: P, T, r, M(r), and L are solved with the help of the equation of state which provides a relation between P, T, and rho (the density). The manner in which the equation of state is implemented by different stellar evolution codes is not fixed. In the interior of the Sun, where hydrogen and helium are fully ionized, the simple ideal gas law provides an adequate equation of state. This is not adequate in the outer layers where minimally the equation of state must account for the hydrogen and helium ionization regions. Historically this was accounted for using the Saha equation. Today though modern calculations utilize the equation of state tables of the OPAL group at Lawrence Livermore.
Nuclear Reactions
The nuclear reaction network followed in most stellar evolution programs includes the hydrogen to helium burning reactions, i.e. ppI, ppII, ppIII chains and the CNO bi-cycle. Other reactions such as helium burning are typically included in stellar evolution calculations but are not important for the Sun. Light element burning of, for example, Li, does not significantly affect the total energy output, hence, the corresponding nuclear reaction chains are not generally included in the stellar evolution reaction network. The reaction network includes all the pp hydrogen burning reaction chains summarized below (Guenther and Demarque 1998).
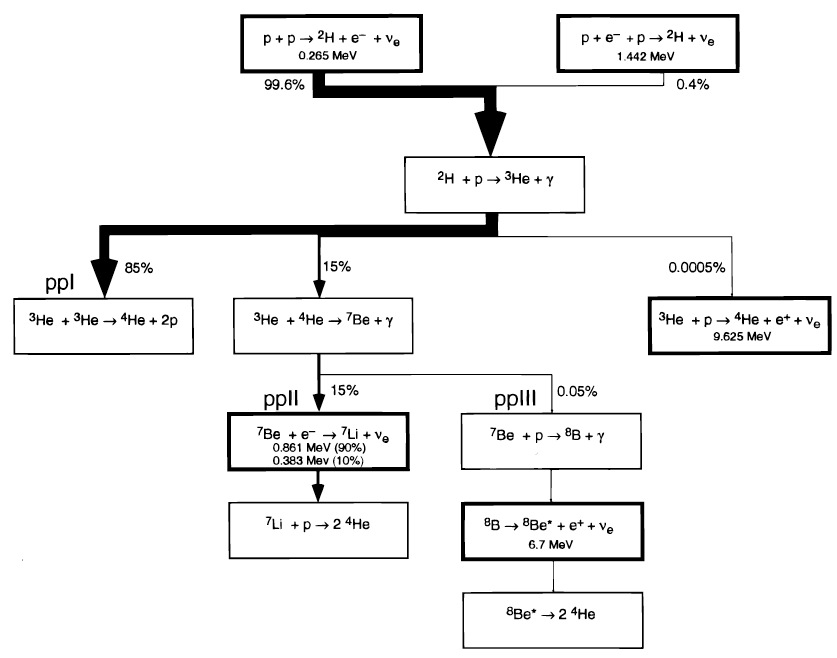
The cross sections or reaction rates, with the exception of the ppI chain, are determined in the laboratory and extrapolated to the temperature density regime encountered in the Sun. Unless a resonance exists, which can significantly increase the cross section, the cross sections are believed to be well determined with an error of ±1% (Parker 1986).
The reaction equations serve two purposes: (1) they determine the energy output per unit time of a given shell, and (2) they determine the evolution of the abundances of the elements involved in the nuclear reactions, such as hydrogen and helium. The former is used in the energy balance equation, and the later is used to specify the evolution of the mean molecular weight in a given shell.
The reaction network equations are kept distinct from the four partial differential equations describing the physics of the model. Nuclear reaction rates are calculated for each shell based on the shell's temperature and density. The new composition is then calculated. The energy output of the shell and its "evolved" composition are then input as constants into the four stellar evolution equations.
Opacities
The tables of Rosseland mean opacities, a function of density, temperature, and composition, used in stellar evolution, are obtained from detailed numerical calculations. Two groups, one at Los Alamos and the other at Lawrence Livermore, currently provide opacity tables. Due to the complexities inherent to the construction of opacities, the opacities potentially represent the most significant source of error in the construction of the standard solar model. The errors in the bound-free opacities have been estimated to be of the order of 20%, although, they may "only" have an error of 10% in the solar interior (Demarque, Christensen-Dalsgaard, Guenther 1988).
Constraints
The standard solar model is distinguished from models of other stars by the constraints imposed on the model. The standard solar model must have the Sun's luminosity and radius at the Sun's age. The basic constraints of mass, radius and luminosity are directly measurable. The accuracy of the mass determination depends directly on the determination of G. The mass of the Sun is 1.9891E33 g with a relative uncertainty of ±0.02% (Cohen and Taylor 1986). The radius of the Sun for stellar structure calculations is defined at an optical depth of tau = 2/3, and is known, through transit and eclipse measurements to be 6.96E10 cm at tau = 0.001 (Ulrich and Rhodes 1983) with and error of ±0.01%. Here, as noted by Ulrich and Rhodes, it is important to translate the glancing angle measurements at the Sun's limb to determine the Sun's radius to a tau = 2/3 optical depth measured perpendicular to the Sun's surface. The luminosity is determined from solar constant measurements from space on both the Nimbus 7 and the SMM satellites: ERB-Nimbus 7 measures 1371.0±0.765 W/m² and SMM/ACRIM measures 1367.7±0.802 W/m² (Hickey and Alton 1983). The luminosity of the Sun is 3.846E33 erg/s from SMM/ACRIM and 3.857E33 erg/s from ERB-Nimbus 7. Taking the average of the two and setting the error equal to the difference between them, one obtains Lsun = 3.8515±0.011E33 erg/s.
The age of the Sun is inferred from the ages of the oldest meteorites. Although, the age is commonly quoted as being 4.6 Gyr or 4.7 Gyr, Guenther (1989) rederived the age using more current information and obtains 4.49±0.04 Gyr. Guenther notes that the latest determinations of the ages of the oldest meteorites (see discussion by Tilton 1988) sets the age of meteoritic condensation at 4.56 Gyr which revises his earlier age estimate. The best meteoritic estimate of the Sun's age is now 4.52±0.04 Gyr.
The abundances of most of the elements can be directly determined from the photospheric spectrum of the Sun. Although, the abundance measurements represents the surface abundances of the Sun and not the interior abundances, it is assumed that these abundances are identical to the abundance of the elements in the zero age model (with the exception of Li and Be which are affected by nuclear burning and diffusion). The inert gases helium, neon, and argon are not visible in the photospheric spectrum hence their abundances must be inferred. Neon and argon abundances are adopted from their measured abundances in the solar corona, solar winds, nebula, and hot stars (Meyer 1979). Helium, as the second most abundant element in the Sun, is left as a free parameter of the standard solar model. Because the luminosity of a stellar model is very sensitive to the mean molecular weight (L proportional to µ^7.5) the abundance of helium is adjusted to produce a solar model with the Sun's luminosity.
Modeling Procedure
The standard solar model is constructed through an iterative procedure. An initial zero age model with a guessed mixing length parameter and helium abundance is evolved to the current age of the Sun. The model's luminosity and radius are then compared to the Sun's. Based on the discrepancy between the model's and the Sun's radius and luminosity, corrections to the mixing length parameter and helium abundance, respectively, are calculated.
The accuracy to which the standard solar model is required to match the observed values of luminosity and radius is determined by the specific application. Historically the standard solar model was used primarily to calibrate the unknown helium abundance and mixing length parameter were determined. Because the accuracy of stellar observations rarely exceeds ±1% in the Log(Teff) - Log (L/Ls) plane, no attempt was made to construct a standard solar model (or stellar model) to a greater precision than ±1%.
Recently the spectrum of p-modes have been used to test and constrain the standard solar model. The frequencies are measured to a remarkable accuracy of ±0.01%. Where 300 shells were enough to achieve the desired reproducible accuracy required for stellar evolution applications, 1500 shells are now required for solar pulsation work. Not only have the number of shells been increased but also their distribution. Most stellar evolution programs distribute shells based on what is happening in a particular region. If, for example, hydrogen is near exhaustion in the core, then the program will increase the number of shells in this region and conversely, the program will reduce the number of shells in the convective envelope. The requirements of solar pulsation are different. Because most p-mode oscillations are confined to the surface layers and because the frequency of their oscillation is primarily determined by the sound speed in these layers more shells are required in the outer layers.
Conclusions
Overall the standard solar model does reflect the level of our knowledge with respect to the established physical processes involved in the evolution of a solar-type star. The model can be improved by attacking the weak points of the model, viz. the opacities, the equation of state, the nuclear reaction cross sections, the convective modeling, the element abundance determinations, and the atmospheric structure. The model can also be improved by adding new physics to the description including the effects of rotation, element diffusion, and magnetic fields.
The standard solar model has evolved significantly from the time of Lane's first model and so has our understanding of the Sun's interior. The diagnostic ability of both the solar p-mode oscillation spectrum and the spectrum of solar neutrino flux observations cannot help but to continue raising the standard of the standard solar model.
References
Böhm-Vitense, E. 1958, Über die Wasserstoffkonvektionszone in Sternen verschiedener und Effektivtemperaturen und Leuchtkräfte, Zeit. f. Astrophys., 46, 108-143.
Chandrasekhar, S. 1939, An Introduction to the Study of Stellar Structure, (New York: Dover Publications).
Clayton, D. 1968, Principles of Stellar Evolution and Nucleosynthesis, (New York: McGraw-Hill Book Company).
Cohen, E. R. and Taylor, B. N. 1986, The 1986 Adjustments of the Fundamental Physical Constants, Codata Bulletin No. 63, (New York: Pergamon Press).
Cox, J. P., and Giuli, R. T. 1968, Principles of Stellar Structure, (New York: Gordon and Breach, Science Publishers).
Davis, R. Jr. 1978, The Solar Neutrino Experiment, in Proceedings of Informal Conference on Status and Future of Solar Neutrino Research, ed. G. Friedlander (Brookhaven National Laboratory Report No. 50879, Vol. 1, 1-33.
Demarque, P., Christensen-Dalsgaard, J. and Guenther, D.B. 1988, GONG Solar Model Workshop, Yale Center for Solar and Space Research, May 27-29, 1987, Comments on Astrophys., 12, 157-163.
Eddington, A. S. 1926, The Internal Constitution of the Stars (Cambridge at the University Press).
Guenther, D. B. 1989, Age of the Sun, Astrophys. J., 339, 1156-1159.
Hickey, J. R. and Alton, B. M. 1983, in Solar Irradiance Variations of Active Region Time Scales, NASA Conference Publication 2310, ed. B. J. LaBonte, G. A. Chapman, H. S. Hudson and R. C. Wilson, p.43.
Meyer, J. P. 1979, The Argon and Neon Abundances in the Solar Neighborhood, in Les Eléments et leurs Isotopes dans L'Univers, Proceedings of 22nd Liège International Astrophysical Colloquium, Institut d'Astrophysique, Université de Liège, 477-489.
Parker, P. 1986, Thermonuclear Reactions in the Solar Interior, in Physics of the Sun, Vol. I, ed. P. A. Sturrock (New York: Reidel), 15-32.
Prandtl, L. 1952, Essentials of Fluid Dynamics (New York: Hafmen), pp. 452.
Schwarzschild, M. 1965, Structure and Evolution of the Stars, (New York: Dover Publications).
Tilton, G. R. 1988 Age of the Solar System, in Meteorites and the Early Solar System, ed. John F. Kerridge and Mildred Shapely Mathews, (Tucson: University of Arizona Press), 259-275.
Ulrich, Roger K. and Rhodes, Edward J., Jr. 1983, Testing Solar Models with Global Solar Oscillations in the 5-minute Band, Astrophys. J., 265, 551-563.